Here we go again with some baffling stuff. I wanted to understand the implications of drug (i.e., medicine or medication) half-lives, in particular for drugs taken daily. The half-life calculators that I found were not useful at all, so I created my own (including an interactive graph), for use on a desktop or laptop, with a keyboard and biggish screen:
http://com.hemiola.com/half-life/
This page does not explain what a half-life is. There are plenty of other sites that do that.
For drugs with a short half-life (e.g., a few hours), I can see how if taken daily, there is no buildup because the daily residual is negligible. It was intuitively obvious to me that with a long half-life (e.g., a half-day or more), taking the drug daily would cause an overlap and buildup—convergent, but still, you would have more drugs in your system than you take daily, and I wanted to know that number.
The basics
Wikipedia recently instituted a format for its drug entries that includes the drug’s half-life. That makes it easy and convenient to look up the half-life for all the drugs I’ve checked.
The basic idea is that if doses overlap (i.e., taken again before the earlier dose[s] leave the system), they stabilize in the system at a higher dose than what you take each time. Also, on a different point, there seems to be an assumption that drugs with a long half-life are slower acting (i.e., weaker). I find that interesting.
The math
There is the Wikipedia page on biological half-life, but the math there is way beyond me. Here is what was obvious to me:
After x hours with half-life H (in hours) and dose D1, the fractional amount D2 leftover is:
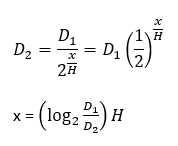
When you take drugs at regular intervals, there might be some nonnegligible amount left over from previous doses. Here is essentially what my calculator is doing, where p is the hours between doses:
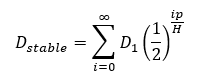
The disclaimers
Yes, I realize the real-world implications of drugs and their half-lives are way more complicated than a simple power-of-two equation. Still, I wanted a quick and easy way to compute the oversimplified numbers.
A few notes about the user interface
- Units don’t matter. Quantities are just numbers. Units need to be consistent; that is all.
- Dosage: the UI uses mg, but you can mentally substitute a different unit.
- Durations: the UI uses hours, but you can mentally substitute a different unit. Yes, the UI divides by 24 to get (assumed) days; that’s because the half-lives I’ve been interested in could be expressed in hours.
- The arrow keys work as a convenience for incrementing and decrementing values, but you can edit the values by typing or pasting, too.
- The time for a logarithmic function to level off is infinite (asymptotic). The percentage elimination sets the point (near 100%) that you want to consider close enough to 100% (of the elimination) to be considered eliminated. For example, it might take 6 days for elimination to reach 97%, which to me is more useful than saying 100% elimination is always (mathematically) infinite.
At what point does a drug stop being effective and get flushed out in your urine, leaving no trace? Different drugs are different. I want to emphasize that I created the UI to show the sum of residuals, not to take other real-life things into account.
I’m now learning that there are drugs that are effective for about four hours or less, with half-lives of 15 – 30 hours. If you take them based on effectiveness (and why wouldn’t you?), there’s massive build-up in your system that no one seems to acknowledge.
An example
Aimovig was approved by the FDA on 2018-05-17. It’s taken once per month, and this really got me wondering, because I’m used to thinking about things taken about once per day. Aimovig’s half-life turns out to be a whopping 28 days (672 hours)! Being that you take it once per half-life, the swing in your system is 70 – 140 mg, even though you take 70 mg per month. Once stabilized after six doses, it takes about 170 days to leave your system, which is a serious commitment!
See also
Some valuable links:
Leave a Reply